みなさん、こんにちは。
今日も「改訂版 チャート式 解法と演習 数学I + A 数研出版」をやっていて、「え？こんな解法かぁ…」と思ったものがありました。解答で示されている因数分解も確かに正しいのですが、私には少しイメージが難しいと思います。みなさんは次の式の展開をどう思われますか？まずは解答に示されている二通りの解法を書いてみます。
出典:「改訂版 チャート式 解法と演習 数学I + A 数研出版」より２５ページ、PRACTICE 20 の(1)の問題。

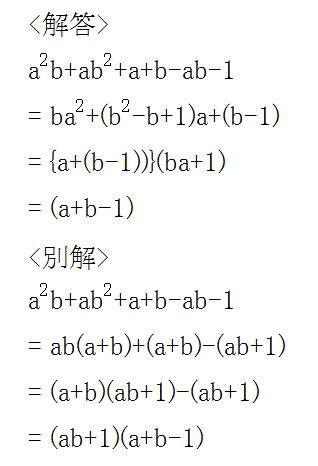
個人的には始めに示されている解法では二行目から三行目への展開が見通せません。しかしこの参考書の一番の解答例なのです。参考書を作成した意図としては、この解法を一番に身に付けた方が良いと考えているのでしょう。確かにこの解法は たすき掛け と言う解法を良く身に付けないとイメージできないと思います。イメージが湧くようにするために、二行目と三行目の間にもう一つ変形式を追記してみましょう。こうしたら、私にも因数分解までたどり着けるようになりました。その変形式を横に追記してみました。

こうすれば、たすき掛け の考え方がしやすくなって、因数分解もし易くなります。

ところで、別解とはまた違った、もっとスマートに因数分解ができる別解も見つけました。それがこちら。

どのような方法で因数分解をするかは自由だと思います。しかし書籍「改訂版 チャート式 解法と演習 数学I + A 数研出版」の意図としては先程も言ったように、やはり たすき掛け と言う考え方で因数分解が出来るようになった方が良い、と言う意図があると思います。
もちろんすべての解法が出来るに越した事はありませんよね、みなさん…。
では今日はこの辺で。