時空 解 さんの日記
2018
4月
14
(土)
10:30
本文
皆さん、おはようございます。時空 解です。
昨日までに予定の積分法に入れませんでした。微分法の最後の練習問題 p108-4 に悩まされました。
この練習問題4、自分に取って難しかったです。
どうも自分は \( x:y \) と言った比で表すところが苦手のようです。ましてやこの問題、変数が2つありますからね…。
どうも自分は \( x:y \) と言った比で表すところが苦手のようです。ましてやこの問題、変数が2つありますからね…。
練習問題 p108-4 は2つの変数、円の半径 と 高さ をどう方程式に落とすかが、まずはカギだと思います。
それにこの問題は方程式を立てられれば、後はそれを微分してグラフから極値を求めれば、最大値 (体積の最大値が求められるのですが…
さて、変数が2つ含まれている形で微分して、それで良いのか?
それもポイントでしょう。
私は「やっぱりこの解法ではダメかなぁ…」と思ってしまい、最後までやってみる事をためらってしまいました。
みなさんはいかがてしたかね?
それにこの問題は方程式を立てられれば、後はそれを微分してグラフから極値を求めれば、最大値 (体積の最大値が求められるのですが…
さて、変数が2つ含まれている形で微分して、それで良いのか?
それもポイントでしょう。
私は「やっぱりこの解法ではダメかなぁ…」と思ってしまい、最後までやってみる事をためらってしまいました。
みなさんはいかがてしたかね?
問題は下記のとおり
これって、まずは円柱の体積の方程式が分からないといけませんよね。
円錐の中に内接する円柱の体積を \( V \) とすると、
円柱の公式は、一般的に
\( V = \pi r^2h \)
ですよね。
問題の答えにも、この比例関係が利用されています。
これを理解する事が、なかなか出来なかったんですよね、私…。
でも、この比の取り方が分れば、円柱の体積 \( V \) の方程式を立てる準備が整います。
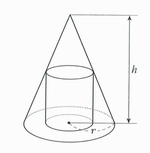
右の図のように、底面の半径が \( r \),
高さが \( h \) の円錐に円柱が内接しています。
このとき、円柱の体積の最大値を求めなさい。
これって、まずは円柱の体積の方程式が分からないといけませんよね。
円錐の中に内接する円柱の体積を \( V \) とすると、
円柱の公式は、一般的に
\( V = \pi r^2h \)
ですよね。
さて、問題文ではこの \( r \) と \( h \) は "円錐の底面の円の半径" と "高さ" を表すのに既に使用されています。ですから円柱の半径と高さを別の変数で表す必要がありますが、これをどう表すか?
それに悩まされました。
私はここで挫折…
答えを見たのですが…それでもしばらくは分かりませんでした。
それに悩まされました。
私はここで挫折…
答えを見たのですが…それでもしばらくは分かりませんでした。
難しい。
とにかく答えには円柱の半径を変数 \( x \) 、高さを変数 \( y \) で表記していました。
まずはそれに従って方程式を立ててみましょう。
\( V = \pi x^2y \)
でもこの方程式にはまだ中身がありません。\( x \) と \( y \) が定まらないからです。\( r \) と \( h \) で \( x \) と \( y \) を表さす必要があります。ここで比の考え方が出て来ます。
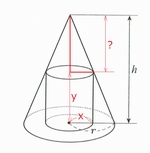
はじめに左図をみて、\( x \) と \( y \) を \( r, h \) で表わそうとしましたが、直接的には、比は見当たりませんよね。でも
\( r : h = x : ? \)
と言う比は見えますよね。ですから \( ? \) を何とか \( h \) と \( y \) で表すしかありません。そこで
\( ? = h-y \)
を利用します。そうすると
\( r : h = x : (h-y) \)
となります。
まずはそれに従って方程式を立ててみましょう。
\( V = \pi x^2y \)
でもこの方程式にはまだ中身がありません。\( x \) と \( y \) が定まらないからです。\( r \) と \( h \) で \( x \) と \( y \) を表さす必要があります。ここで比の考え方が出て来ます。

はじめに左図をみて、\( x \) と \( y \) を \( r, h \) で表わそうとしましたが、直接的には、比は見当たりませんよね。でも
\( r : h = x : ? \)
と言う比は見えますよね。ですから \( ? \) を何とか \( h \) と \( y \) で表すしかありません。そこで
\( ? = h-y \)
を利用します。そうすると
\( r : h = x : (h-y) \)
となります。
問題の答えにも、この比例関係が利用されています。
これを理解する事が、なかなか出来なかったんですよね、私…。
でも、この比の取り方が分れば、円柱の体積 \( V \) の方程式を立てる準備が整います。
\( V = \pi x^2y \) …(1)
\( r : h = x : (h-y) \) …(2)
\( r : h = x : (h-y) \) …(2)
まず (2) を整理して、\( y = \) の形にしてみましょう。
\( r : h = x : (h-y) \) …(この式から内項と外項を掛ける)
\( r(h-y) = hx \)
\( rh-ry = hx \)
\( -ry = hx -rh \)
\( -ry = -h(r-x) \)。
最後に両辺を \( -r \) で割ると
\( y = \displaystyle \frac{h}{r}(r-x) \) …(2)'
となりますよね。
\( r : h = x : (h-y) \) …(この式から内項と外項を掛ける)
\( r(h-y) = hx \)
\( rh-ry = hx \)
\( -ry = hx -rh \)
\( -ry = -h(r-x) \)。
最後に両辺を \( -r \) で割ると
\( y = \displaystyle \frac{h}{r}(r-x) \) …(2)'
となりますよね。
この \( y \) の式を (1) に代入すると、\( V \) の方程式から得られます。
\( V = \pi x^2 \displaystyle \left\{\frac{h}{r}(r-x) \right\} \)
上式を展開すると
\( V = \pi h x^2- \displaystyle \frac{\pi h x^3}{r} \)
となります。
\( V = \pi x^2 \displaystyle \left\{\frac{h}{r}(r-x) \right\} \)
上式を展開すると
\( V = \pi h x^2- \displaystyle \frac{\pi h x^3}{r} \)
となります。
さて、皆さん。
この上式が得られたとしても、これから円柱の最大値をどう導き出すか分かりますか?
変数が \( x \) と、それから \( h \) も変数なんですよ。
私はここで怖気づきました。この \( V \) の方程式を \( x \) で微分しても極大値が求められるとは思えなかったのです。
でも、この練習問題4の答えは、この式を \( x \) について微分して極大値を導いています。
やっぱりやってみないと分からないものですよね。
直感的には疑問を感じても、一度はやってみるものです。
この上式が得られたとしても、これから円柱の最大値をどう導き出すか分かりますか?
変数が \( x \) と、それから \( h \) も変数なんですよ。
私はここで怖気づきました。この \( V \) の方程式を \( x \) で微分しても極大値が求められるとは思えなかったのです。
でも、この練習問題4の答えは、この式を \( x \) について微分して極大値を導いています。
やっぱりやってみないと分からないものですよね。
直感的には疑問を感じても、一度はやってみるものです。
\( V \) の方程式を \( x \) について微分すると下記のようになります。
\( \displaystyle \frac{dV}{dx} = 2 \pi h x - \frac{3 \pi h x^2}{r} = \pi h x \left( 2- \frac{3x}{r} \right) \)
\( \displaystyle \frac{dV}{dx} = 0 \) のとき、\( x = 0, \displaystyle \frac{2}{3}r \)
\( \displaystyle \frac{dV}{dx} = 2 \pi h x - \frac{3 \pi h x^2}{r} = \pi h x \left( 2- \frac{3x}{r} \right) \)
\( \displaystyle \frac{dV}{dx} = 0 \) のとき、\( x = 0, \displaystyle \frac{2}{3}r \)
ここまでくれば、あとはいつものようにグラフの増減を確認にて極大値を求めるだけです。
もうこんな時間になってしまいました。
すみません、後は皆さんでやってみて下さいね。
もうこんな時間になってしまいました。
すみません、後は皆さんでやってみて下さいね。
では今日も1日の習慣を実施します。小さな一歩・挑戦を試みます。
応援してね。
千里の道も一歩から。そしてその道は登り坂です。ローマは1日にして成らず、です。
(ポチッとブログ村のバナーをクリックしてね) ![]()
![]()
| ★ 習慣作りのための、小さな課題 | ☆ 昨日の実施状況 |
|---|---|
| そろばんの練習5問 (暗算の獲得) ブログ投稿後 |
宮田 輝 そろばん教室 加減算編 見取算問題1 (1)~(16)三連続1回 ( 通しはせず ) |
| 斜め懸垂1回 (ボルダリングの体力獲得) &fnbsp; 朝食前 |
斜め懸垂12回、グリップ25回、腕立て15回、腹筋15回 |
| チャート式参考書1問 (物理学の数式の理解力の獲得) 朝食後9時から |
白II+B:数学検定( 4/15 )までお休み 青I+A:数学検定( 4/15 )までお休み 実用数学技能検定 要点整理 2級:第5章の微分法 練習問題 p108(2)(3)(4) |
| 心の筋トレ (集中力の獲得) 習慣を実行するにあたって |
今朝・7時に布団から出る:7時51分 --- ブログの投稿 --- 昨日・朝食は台所でとって2階へ:× 昨日・机に座ったら、直ぐに学習用具を開く:× 昨日・理数の解法を楽しむ:〇 昨日・夜食も台所でとって2階に:× (またプレバトの続きを観てしまった) 昨日・夜は23時に布団に入る:午前00時23分 |
閲覧(8653)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記