時空 解 さんの日記
2018
5月
29
(火)
09:05
本文
皆さん、おはようございます。時空 解です。
昨日の夜に、書籍「定理のつくりかた」の第3部を最後まで読みました。この第3部は "ピックの定理" を実際に証明してゆくところです。
定理をつくるのって、本当に地味な作業が続くんですね。この第3部を読んでいてつくづくそう思います。でも、地味な作業に入る前に、数学的な閃きと言うか解法に向かう方向性が頭にピンと来ないと、地味な作業に進めないことも見て取りました。それに正しい方向性が閃くためには、その前に手探りで「こうかな?」と予想する仮作業を繰り返すこともしばしばでしょう。
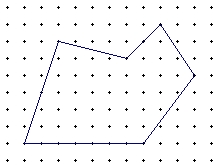 ビックの定理を例にとると、
ビックの定理を例にとると、
この試行錯誤を乗り越えて、ピックの定理は最終的に下記の形をしています。
$ {\displaystyle S=i+{\frac {1}{2}}b-1} $
ここで $ i $ は格子多角形の内部にある格子点の個数、$ b $ は格子多角形の辺上にある格子点の個数です。
格子の数を数える、と言う事が「簡単に」と言う抽象的な部分の答えになっています。
ピックの定理を造る…前例がなければ、私には達成できそうにありませんね。それが率直な感想です。すでに確立されている道筋を学ぶだけでも、途中、計算間違いや記号の書き間違い、書き損じなんかをしたら、それだけでまわり道をする事になります。一度書籍を読んでも、独りではピックの定理を造るための証明を再現できないでしょう。
この第3部を読んでいると、数学の定理を作ることって、小説家が作品の1つを完成させるの同じような苦労があるなぁ、と思いました。芸術作品と同じように毎日少しづつ作業を進めて行くものなのですね。
ところで、ピックの定理の証明を書く ( 人に伝える ) 段階で "累積帰納法" と言うテクニックを使いますが、じつは私には、この部分が理解不能でした。悔しいですが、一般的な帰納法に付いても勉強不足の私です。ましてや、その帰納法を一歩進めた累積帰納法です。これから数学検定の学習に合わせて学んで行きたいと思っています。
ピンとくるようになるには高校数学の2年生で学ぶ数列に早く取り組まないとダメですね。数列の中で帰納法と言うのは出て来ます。
そういえば皆さんは、第322回 ( 7月22日(日) ) の数学検定の申し込みはもうされましたか?私は2日前にネットから申し込みを済ませましたよ。
では今日も1日の習慣は実施します。小さな一歩・挑戦を試みます。
昨日の夜に、書籍「定理のつくりかた」の第3部を最後まで読みました。この第3部は "ピックの定理" を実際に証明してゆくところです。
定理をつくるのって、本当に地味な作業が続くんですね。この第3部を読んでいてつくづくそう思います。でも、地味な作業に入る前に、数学的な閃きと言うか解法に向かう方向性が頭にピンと来ないと、地味な作業に進めないことも見て取りました。それに正しい方向性が閃くためには、その前に手探りで「こうかな?」と予想する仮作業を繰り返すこともしばしばでしょう。
 ビックの定理を例にとると、
ビックの定理を例にとると、
と言う命題のなかの「簡単に」の部分がそれに該当します。この「簡単に」をどのような形で実現するか?それを実現するため方向性を確信するには、試行錯誤の連続です。格子多角形の面積を簡単に計算する方法を見つけよ。
この試行錯誤を乗り越えて、ピックの定理は最終的に下記の形をしています。
$ {\displaystyle S=i+{\frac {1}{2}}b-1} $
ここで $ i $ は格子多角形の内部にある格子点の個数、$ b $ は格子多角形の辺上にある格子点の個数です。
格子の数を数える、と言う事が「簡単に」と言う抽象的な部分の答えになっています。
ピックの定理を造る…前例がなければ、私には達成できそうにありませんね。それが率直な感想です。すでに確立されている道筋を学ぶだけでも、途中、計算間違いや記号の書き間違い、書き損じなんかをしたら、それだけでまわり道をする事になります。一度書籍を読んでも、独りではピックの定理を造るための証明を再現できないでしょう。
この第3部を読んでいると、数学の定理を作ることって、小説家が作品の1つを完成させるの同じような苦労があるなぁ、と思いました。芸術作品と同じように毎日少しづつ作業を進めて行くものなのですね。
ところで、ピックの定理の証明を書く ( 人に伝える ) 段階で "累積帰納法" と言うテクニックを使いますが、じつは私には、この部分が理解不能でした。悔しいですが、一般的な帰納法に付いても勉強不足の私です。ましてや、その帰納法を一歩進めた累積帰納法です。これから数学検定の学習に合わせて学んで行きたいと思っています。
ピンとくるようになるには高校数学の2年生で学ぶ数列に早く取り組まないとダメですね。数列の中で帰納法と言うのは出て来ます。
そういえば皆さんは、第322回 ( 7月22日(日) ) の数学検定の申し込みはもうされましたか?私は2日前にネットから申し込みを済ませましたよ。
では今日も1日の習慣は実施します。小さな一歩・挑戦を試みます。
応援してね。
千里の道も一歩から。そしてその道は登り坂です。ローマは1日にして成らず、です。
(ポチッとブログ村のバナーをクリックしてね) ![]()
![]()
| ★ 習慣作りのための、小さな課題 | ☆ 昨日の実施状況 |
|---|---|
| そろばんの練習5問 (暗算の獲得) ブログ投稿後 |
宮田 輝 そろばん教室 加減算編 見取算問題10 (1)~(6) 通し3回連続1回 |
| 斜め懸垂1回 (ボルダリングの体力獲得) &fnbsp; 朝食前 |
斜め懸垂12回、腕立て15回、腹筋15回、グリップ30回 |
| チャート式参考書1問 (物理学の数式の理解力の獲得) 朝食後9時から |
白II+B:p323~p325 青I+A:できず |
| 心の筋トレ (集中力の獲得) 習慣を実行するにあたって |
今朝・7時に布団から出る:7時02分 --- ブログの投稿 --- 昨日・朝食は台所でとって2階へ:〇 昨日・机に座ったら、直ぐに学習用具を開く:〇 昨日・理数の解法を楽しむ:〇 昨日・夜食も台所でとって2階に:× 昨日・23時にキューピーコーワ i プラスを飲む:〇 昨日・寝床に入った時間:23時19分 |
閲覧(4776)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



