時空 解 さんの日記
みなさん、こんばんは。
因数分解の問題をやっていて、いい問題があったのでここに書いてみます。
出題はいつものとおり「改訂版 チャート式 解法と演習 数学I+Aー数研出版」です。
今回の問題は 32ページ。Exercisec 24 (5)です。

これは典型的な たすき掛け のテクニックを使って解く因数分解ですが、例題や練習問題とは違って組み合わせを探るのがやっかいです。私は可能性のある数字を書き並べてから検討して行きました。
目標とする因数分解の形は、
( ?a ± ? )( ?a ± ? )
です。
上の式を展開して得られる多項式が、問題(与式)の多項式と同じになれば言い訳です。
と言う事で「?」のところにどんな数字が入るかを見つけなくてはなりません。
まずは a の係数の?について。
多項式に展開すると2次となる a の係数 18 は 2a x 9a かまたは 3a x 6a のどちらかの掛け算の結果として得られる数字です。
( 2a ± ? )( 9a ± ? ) もしくは ( 3a ± ? )( 6a ± ? )
次に、定数項 -7 に対応する?について。
7 は ±1 x ±7 以外にありえません。なので a の係数とこの 7 を考え合わせると、可能性のある因数分解の式は下記の4パターンです。
( 2a ± 1 )( 9a ± 7 ) もしくは ( 3a ± 1 )( 6a ± 7 )、( 2a ± 7 )( 9a ± 1 ) もしくは ( 3a ± 7 )( 6a ± 1 )
さて上の4パターンをみながら、後は符号がプラスなのかマイナスなのか、組み合わせを考えてみました。
問題(与式)の定数項が -7 と言うところから、プラスの整数×マイナスの整数から -7 を作る事はわかりますので
(?a - 7)(?a + 1) もしくは (?a + 7)(?a - 1)
のどちらかだと推測できます。
ここまでのことから、可能性のある因数分解の形は下記の組み合わせ8個が考えられます。
( 2a - 1 )( 9a + 7 ) もしくは ( 3a + 1 )( 6a - 7 )、( 2a - 7 )( 9a + 1 ) もしくは ( 3a + 7 )( 6a - 1 )
( 2a + 1 )( 9a - 7 ) もしくは ( 3a - 1 )( 6a + 7 )、( 2a + 7 )( 9a - 1 ) もしくは ( 3a - 7 )( 6a + 1 )
後は a の一次の項 -39 を考え合わせて、8個のうちのどれかを探しました。
-39a = (6a 掛ける -7) + (3a 掛ける 1) = -42a + 3a
可能性を書き並べることで、解答にたどり着きました。答えは
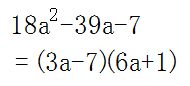
です。
この問題はちょっと厄介でしたが、みなさんはいかがでしたか?
では今日はこの辺で。
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



