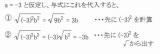みなさん、こんにちは。
早速ですが、みなさんは下記の問題を解く事が出来るでしょうか？

申し訳ありせん、実は上記の問いは、不完全な問いの形で出題させて頂いています。しかしそれに気が付いた方はいらっしゃるでしょうか。もしいらっしゃるとしたら、その方はきっと数学に造詣が深い方か、数学を生業にされているかたなのではないかと思います。
上記の出題には、a , b の変数が負数か正数かの指定が必要です。
正式な出題の形で書くとするとこうなります。

a と b の変数の符号が分かれば、この出題に正確に答えることが出来ます。答えは下記になります。

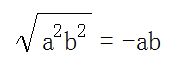
では、あらためてご質問ですが、みなさんはこの答えに納得が出来るでしょうか？私は納得が出来ない方も少なからずいらっしゃるのではないかと思っています。何故かと言えば、私もその中の一人なのだから・・・。

しかしこれは正しい解答なのです。「改訂版 チャート式 解法と演習 数学Ⅰ+Aー数研出版」の３６ページの基本例題１８の (4) として、ちゃんと解説されている問題なのです。書籍に示されている解説は下記のとおりです。

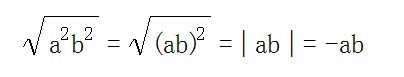
しかし、これで納得が出来る方がいるのでしょうか？私は疑問です。それにこの解説は、実は解説に使えるページ数の関係で、絶対値記号を持ち込んでうまく誤魔化しているのではないか、と思ったりもいたします。ともかく、私はこの解説には納得しておりません。
しかし自分なりに納得の出来る仕方は頭に浮かびました。
私のなりの納得の仕方を、これから下記に示したいと思います。

まずは、どんな点で納得が行かないのか？その説明からいたします。
 

疑問点

上記のごとく、①のようにルートの中の ( -3 ) の二乗を先に計算してからルートを取ると、答えは -3b になりません。 -ab にはならないと言う事です。
「改訂版 チャート式 解法と演習 数学Ⅰ+Aー数研出版」は ② のように式を変形するのが正しいとしていますね。解説の如く、絶対値表現を持ち出してきて、そのややこしさを回避しているように思われます。絶対値表現で納得できましたか？みなさま・・・？
こんな事をせずに潔く、例えば・・・そう、あくまでも例えばですけど、こんな説明をすれば良いと思います。
「 a は負数なのか正数なのか？それを壊さないように式を変形する事が、数学の記法を保つための暗黙の了解です」
実は私はこれが本当の理由なのだと思っています。それとも、演算子の優先順位の問題でしょうかね？
例えば一つの式の中に掛け算と足し算かあったとすると、掛け算の方を先に演算するのが、演算子の優先順位ですよね。それと同じように、指数演算よりもルート演算の方を先に行なう、と言うような演算子の優先順位という物があったでしょうか？これはちょっと調べてみたのですが、ありそうにないですね。
( 参考:ウィキペディア、演算子の優先順位 )
もし有ったとしたら間違いなく、「改訂版 チャート式 解法と演習 数学Ⅰ+Aー数研出版」のここの問題で解説している事でしょう。

ともかく、とある変数( 例えば a )が有ったとして、これに指数計算やルート計算を行なった結果がもともとの正負の記号と変わってしまうようでは、それで数学が破綻します。それを防ぐ意味でも、もともの変数が負数なのか正数なのか、常に意識する必要がある、と言う事ですね。

いろいろな意味で「改訂版 チャート式 解法と演習 数学Ⅰ+Aー数研出版」の３６ページの基本例題１８の (4) はとても重要な問題だと思った次第です。ここのブログに残しておきたいと思います。
では今日はこの辺で。