皆さんこんにちは、時空 解です。 今日はマスペディア 1000 のトピック 3１０,３１１について書いてみたいと思います。 この二つのトピックで書かれているのは、あの有名な「四色問題」です。 トピック 3１０と３１１には、この「四色問題」のポイントだけがシンプルに書かれています。 まずは 四色問題の始まりは英国の弁護士であり数学者でもあったサー・アルフレッド・ケンプが１８７９年に提起した問題である。 と書かれています。 ケンプがはじめに四色で球面上の...

皆さんこんにちは、時空 解です。 今日はマスペディア 1000 からのブログネタです。本当ならば数検も過去問の記事でもと想っていたのですが… 実は今日は朝からとても疲れていますので問題を解く気力があまりなかったんですよね。( ^^; それでちょっと手抜きになりますが、マスペディアからネタを拝借してきました。 でも今回のトピック 309 はちょっと面白いネタでもあります。 2008年に開催された北京オリンピックの水泳競技場、一般には &q...

皆さんこんにちは、時空 解です。 今回はマスペディア1000 から取り上げるトピックは、 ・トピック３０８：ケルヴィン予想 です。 まず "ケルヴィン" と言うのは、私の世代では "ケルビン" と言う発音で名が通っている物理学者ですかね…。 ちなみに温度単位でも "ケルビン" というものがありますよね。 これらはすべてウィリアム・トムソンに関連していることです。 でもブドウパン...

皆さんこんにちは、時空 解です。 今日はマスペディアのトピック 305 ～ 307 から話題を拾います。 トピック 305：超球面充填 トピック 306：六角ハニカム予想 トピック 307：蜂が知らないこと 充填というものは以前にもご紹介したと思います。 例えば果物屋さんがなるべく狭いスペースに多くの みかん を置くためにはどんなふうにみかんを並べたり積み上げたらいいのか？と言うことに関係することです。 ミツバチのハチの巣の形も、そんな例の一つですね...

皆さんこんにちは、時空 解です。 ここ２、３日、朝に急用が入ります。なかなか数学の学習が思うように進められませんので、今日はマスペディア 1000 のトピックを取り上げます。 今回はトピック３０４番、ケプラー予想です。 この予想、私は知りませんでした。( ^^; 恥ずかしいですね、これは有名な予想のようです。 なんと言ってもヒルベルトの２３問のうちの一つにも選ばれているんですよね。 １８番の問題：合同な多面体による空間の構築 さて、問題の概要...

皆さんこんにちは、時空 解です。 今日は "マスペディア 1000" に目を通していて、 「やっぱりこんな事を証明の対象に考えるんだ」 と、自分と偉人との違いを実感しましたので、それについて書いてみたいと思います。 マスペディア 1000 のトピック 303 にこんな問題が提起されています。   コインの入った袋とテーブルがあるとする。ここで、できるだけ多くのコインをテーブルの上に敷き詰めるという問題を解くことにしよう。 ...

皆さんこんにちは、時空 解です。 今日はマスペディア 1000 の中から、トピック 302 をご紹介しましょう。 トピック 302 で紹介されているのは「ピックの定理」です。 朝、マスペディア 1000を開いてこの定理を見た時に 「お！　これはピンと来る定理だな」 と思った次第です。 でもこの定理がどうしてピンと来たのか？ちょっと不思議だったんですが…もしかしたら自分にも数学のセンスが育まれてきたのかな… なんて想って...

皆さんこんにちは、時空 解です。 今日は書籍「マスペディア 1000」から、サイクロイドにまつわるトピックをまとめてご紹介しましょう。 私個人としては、このサイクロイドと言う言葉はよく聞いてはいたのですが、明確な数式や歴史的なことは知りませんでした。 でも、紐を垂らすと、その曲線がどんな曲線になるのか？　…それは放物線ではない、と言うことは知っていましたけどね。 それが懸垂線と言われていて、ライプニッツやホイヘンス、ヨハン・ベルヌーイの手で証明さ...

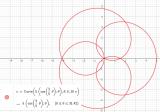
皆さんこんにちは、時空 解です。 今日はちょっと驚くようなグラフをご紹介したいと思います。 まぁ驚くか否かは人それぞれですけどね… ( ^^; とにかく私はちょっと驚きました。下記の方程式をグラフに描くと、右図のような花びら的グラフが出てくるんですね。 ・$ 5 \cos 2 \theta $ まぁ私は下記のようなスクリュー的なグラフの方が好きですが… ・$ 5 \sin 3 \theta $ このグラフは書籍「マ...

皆さんこんにちは、時空 解です。 今日もマスペディア 1000 を読んでいたら、面白いトピックがありました。 トピック 294 です。 ・４匹のネズミの問題　(Mice problem)  これは、４匹のネズミ $ A,~B,~C,~D $ が正方形の部屋の４隅から１匹ずつ出発する (動き出す) 時の、その動きに関することです。 こんなことが数学に関係あるのかって思いませんか？　( ^^; でも、あるみたいなんです。 ４匹は同時に放たれ...

皆さんこんにちは、時空 解です。 最近自分の頭の中が飽和気味になってしまっていました。これは "青チャート式数学" の解法とか "数学検定" ２次問題の記述の仕方に気持ちが捕られているからかも知れません。 まぁ高校数学をキチンと学ぶというのは、数学力を身に付ける大切な学習だと思いますが、楽しさを満喫できなくなる原因かも知れませんね。 そんなこんなで、久々に "マスペディア 1000" を手に取ってみまし...

皆さんこんにちは、時空 解です。 久々にマスペディア 1000 を開いてみました。一番最近に取り上げたのは２０１１年の６月２７日のことでした。 あっと言う間に１０か月が過ぎていたんですね。早い物です。 今回取り上げるのはトピック 292 の「アルキメデスの螺旋」です。 どうして１０か月間もマスペディア 1000 を取り上げなかったのだろうなぁと考えるに、きっと内容が難しくなっているからでしょうね。( ^^; 今回の「アルキメデスの螺旋」に付いても、当時の...

皆さんこんにちは、時空 解です。 今日はマスペディア 1000 のトピック 290 と 291 からの話題です。 高校時代から極座標と言うものは知っていましたが、ずっと関わらないようにしていました。 デカルト座標に馴染んていたせいもあって、極座標に必要性を感じていなかったんです。 まぁ必要性を感じないと言うのは、高校時代にテストに殆ど出題され無かったから、と言うことなんでしょうけどね。 でもこれからもずっと数学の学習を進めて行くとなると、やっぱり必要性は...

皆さんこんにちは、時空 解です。 マスペディア 1000 と言う辞書形式の書籍から、このブログでトピックを時々ご紹介しています。最近ではご紹介の頻度が減っているかも知れませんけどね。 まぁこの「マスペディア 1000」と言うカテゴリーを楽しみにされている方は少ないかも知れません。 なにせ、このカテゴリ―を始めた理由が " ブログネタがない時には「マスペディア 1000」。ここから話題を広げたいと思います。" と言う理由ですからね。...

皆さんこんにちは、時空 解です。 今日は久々にマスペディア 1000 に目を通してみました。 トピックの ・284：楕円面 です。 楕円面と言うとちょっとイメージが湧きませんが、地球の形と言えばイメージが沸くでしょう。 まぁ果物のみかんのような形ですね。 みかんのように地球は極端に球をつぶした形ではありませんが、一般的には遠心力で赤道方向にすこし膨らむイメージが、確かにありますよね。 でも、今日読んだ「トピック 184：楕円面」から、地球の...

皆さんこんにちは、時空 解です。 今日もマスペディア 1000 から、トピック 283 を取り上げてみましょう。前回は「ニュートンの３次曲線」をご紹介しましたが、これは平面上の曲線でしたね。 今回は三次元空間における、曲面に関連することです。 曲面の種類によって、名称が付けられているんですね。今回のトピック 283 に目を通してみて、聞いたような聞いたことないような名称が出てまいりました。 「一葉、二葉双曲面？」 「楕円放物面？」 うーむ&hellip...

皆さんこんにちは、時空 解です。 今日は久々にマスペディア 1000 のトピックからの話題です。 トピック 282 に「ニュートンの３次曲線」が紹介されていました。 ニュートンは $ x^3,~x^2y,~xy^2,~y^3 $ を含む方程式によって定義される曲線である３次曲線に付いて、考察していたそうです。 うーむ…ニュートンって小学生の頃の印象としては物理学者ですけどね。 ここのところ、どんどんと数学者のイメージが増してくるのは私だけで...

皆さんこんにちは、時空 解です。 今日は書籍 スペディア 1000 のトピック 278 ～ 281 に目を通してみました。楕円、放物線、それと双曲線について書かれたトピックです。 これは以前にもご紹介した「円錐曲線」に関連するトピックです。( マスペディア 274 ～ 275 円錐曲線について ) 円錐曲線と言うのは奥が深いんですね。楕円、放物線、双曲線と、三つの曲線の関係を円錐の断面として区別します。 Wikipedia のページに載っている図が分かり易いで...

皆さんこんにちは時空 解です。 今日は久々にマスペディアを開いてみました今日はトピック 277 です。焦点と準線。 ここのトピックを見て驚きましたね。皆さんは焦点と準線と聞いて何をイメージしますか？私はトンとイメージが湧きませんでしたので、まずはパソコンで検索、とりあえずは、Wikipedia を参照してみました。 ・焦点 (幾何学) 　1.2：焦点と X 線を用いた定義 任意の円錐曲線は、一つの焦点と一つの準線（これは焦点を含まない直線の形で与えられる）...

皆さん、おはようございます。時空 解です。 久々にマスペディア 1000 を開いてみました。 トピック第２７６番目は「２次曲線」と言う表題なのですが、ちょっと読んで 「うん…？！」 と思う数式が目に入りました。  $  B^2-4AC  $  マスペディア 1000 によると 「数 $ B^2-4AC $ が曲線の種類決定のカギを握っている」 となっています。 ２次曲線は、一般に $ Ax^2...