時空 解 さんの日記
2021
2月
3
(水)
10:55
本文
皆さんこんにちは、時空 解です。
今日の朝、基本例題84の2つ目の解答が自分なりに分かりました。
まずはチャート式の問題・解答と、2パターンのそれぞれの図を下に示してみます。

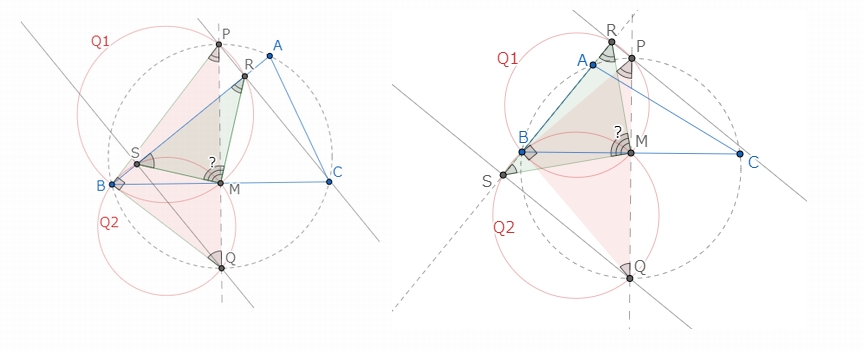
上図の左側がチャート式数学の解答でも使われている図です。右側が別パターンの図になります。
チャート式の解答の図と、右側の図違いは、三角形の頂点Aが垂直二等分線の右側にあるか、左側にあるかの違いです。この違いが微妙に解答の記述方法の違いを生みます。
チャート式の左図の方は、
・円 $ Q2 $ に付いて、四角形の外角として $ \angle RSM = \angle PQB $
が言えてます。
でも、右図の場合は
・円 $ Q2 $ に付いて、弦 $ BM $ の円周角として $ \angle RSM = \angle PQB $
がいえるんでよね…。
うーむ…
この違いに付いて、皆さんはどう想われますか?
天下の青チャート式数学ならばこの2パターンをともに示して欲しい気がするんですが…。まぁチャート式で採用されている解答のほうが「円周角の定理」と「円に内接する四角形の外角の定理」の2つの定理を使えないと解けないパターンなのでね。こちらを選んでいる事には意味があります。
でも2つ目のパターンに付いて、解答に辿り着くのに時間を費やしてしまいました。チャート式の解答にも載せて欲しかったですね。
でも…まぁこれで勉強にもなったと言えば言えますが…。
この問題を考えるに当たって、数学ソフト GeoGebra も少しは使えるようになって来ましたしね。
図形問題って、図をキッチリと書けないとなかなか解けませんしね…。結果オーライですかね。
では今日も休日を始めています。休日の充実こそ、人生の充実です。
今日の朝、基本例題84の2つ目の解答が自分なりに分かりました。
まずはチャート式の問題・解答と、2パターンのそれぞれの図を下に示してみます。


上図の左側がチャート式数学の解答でも使われている図です。右側が別パターンの図になります。
チャート式の解答の図と、右側の図違いは、三角形の頂点Aが垂直二等分線の右側にあるか、左側にあるかの違いです。この違いが微妙に解答の記述方法の違いを生みます。
チャート式の左図の方は、
・円 $ Q2 $ に付いて、四角形の外角として $ \angle RSM = \angle PQB $
が言えてます。
でも、右図の場合は
・円 $ Q2 $ に付いて、弦 $ BM $ の円周角として $ \angle RSM = \angle PQB $
がいえるんでよね…。
うーむ…
この違いに付いて、皆さんはどう想われますか?
天下の青チャート式数学ならばこの2パターンをともに示して欲しい気がするんですが…。まぁチャート式で採用されている解答のほうが「円周角の定理」と「円に内接する四角形の外角の定理」の2つの定理を使えないと解けないパターンなのでね。こちらを選んでいる事には意味があります。
でも2つ目のパターンに付いて、解答に辿り着くのに時間を費やしてしまいました。チャート式の解答にも載せて欲しかったですね。
でも…まぁこれで勉強にもなったと言えば言えますが…。
この問題を考えるに当たって、数学ソフト GeoGebra も少しは使えるようになって来ましたしね。
図形問題って、図をキッチリと書けないとなかなか解けませんしね…。結果オーライですかね。
では今日も休日を始めています。休日の充実こそ、人生の充実です。
閲覧(8206)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



