時空 解 さんの日記
2021
6月
8
(火)
09:22
本文
皆さんこんにちは、時空 解です。
今日の朝、「実用数学技能検定要点整理2級」をやっていたら下記の問題に出くわしました。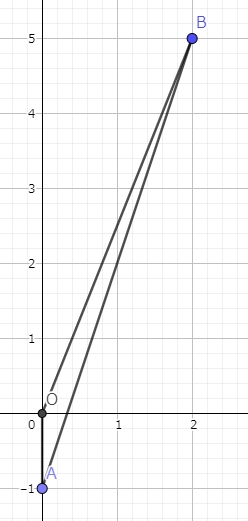
うーむ…これを座標平面上に書き込むと右図のようになります。
この三角形の面積と言えば一目瞭然!
底辺を $ OA $ と見れば、三角形の高さは $ 2 $ ですよね。ですから
$ (1 \cdot 2) \div 2 = 1 $
です。
しかしこれでは簡単すぎないか?
と思いきや答えをみると…なんだ…こんなややこしい解答の仕方が書いてありました。
数学検定の2級2次を受検している時に、この「p42 応用問題 2次 1」のような問題に出くわしたら、上記のように解答しないと1点貰えないのでしょうか?
とやったら何点貰えるのでしょう…?
うーむ…
でも、これは三角形の1辺が座標軸に平行だからできる計算です。実際の数学検定2級2次の出題は、3辺すべてが座標軸と平行でない場合を出してくるのでしょう。
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
今日の朝、「実用数学技能検定要点整理2級」をやっていたら下記の問題に出くわしました。
p42 応用問題 2次 1
座標平面上の3点 $ O(0,0),~A(0,-1),~B(2,5) $ を頂点とする $ \triangle OAB $ の面積を求めなさい。

うーむ…これを座標平面上に書き込むと右図のようになります。
この三角形の面積と言えば一目瞭然!
底辺を $ OA $ と見れば、三角形の高さは $ 2 $ ですよね。ですから
$ (1 \cdot 2) \div 2 = 1 $
です。
しかしこれでは簡単すぎないか?
と思いきや答えをみると…なんだ…こんなややこしい解答の仕方が書いてありました。
2点 $ A,~B $ 間の距離は
$ AB = \sqrt{ (2-0)^2 + \{ 5-(-1) \}^2 } = \sqrt{ 40 } = 2\sqrt{ 10 } $
直線 $ AB $ の式は $ y = 3x - 1 $ すなわち $ 3x - y - 1 = 0 $ だから、原点 $ O(0,0) $
と直線 $ AB $ の距離 $ d $ は、
$ d = \displaystyle \frac{ \left| -1 \right| }{ \sqrt{ 3^2 + (-1)^2 } } = \frac{ 1 }{ \sqrt{ 10 } } = \frac{ \sqrt{ 10 } }{ 10 } $
よって面積は、$ \displaystyle \frac{ 1 }{ 2 } × AB × d = \frac{ 1 }{ 2 } × 2\sqrt{ 10 } × \frac{ \sqrt{ 10 } }{ 10 } = 1 $
答え 1
数学検定の2級2次を受検している時に、この「p42 応用問題 2次 1」のような問題に出くわしたら、上記のように解答しないと1点貰えないのでしょうか?
座標平面上の図を示して
底辺を $ OA $ と見れば、三角形の高さは $ 2 $
従って三角形の面積の公式より
$ (1 \cdot 2) \div 2 = 1 $
答え 1
底辺を $ OA $ と見れば、三角形の高さは $ 2 $
従って三角形の面積の公式より
$ (1 \cdot 2) \div 2 = 1 $
答え 1
とやったら何点貰えるのでしょう…?
うーむ…
でも、これは三角形の1辺が座標軸に平行だからできる計算です。実際の数学検定2級2次の出題は、3辺すべてが座標軸と平行でない場合を出してくるのでしょう。
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
閲覧(7007)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



