時空 解 さんの日記
2023
5月
25
(木)
09:14
本文
皆さんこんにちは、時空 解です。
今日は青チャート数学IIの微分法の中の "関数の増減と極大・極小" について学習をしていたのですが、その時にちょっとびっくりしました。
うーむ…そうなのか…。
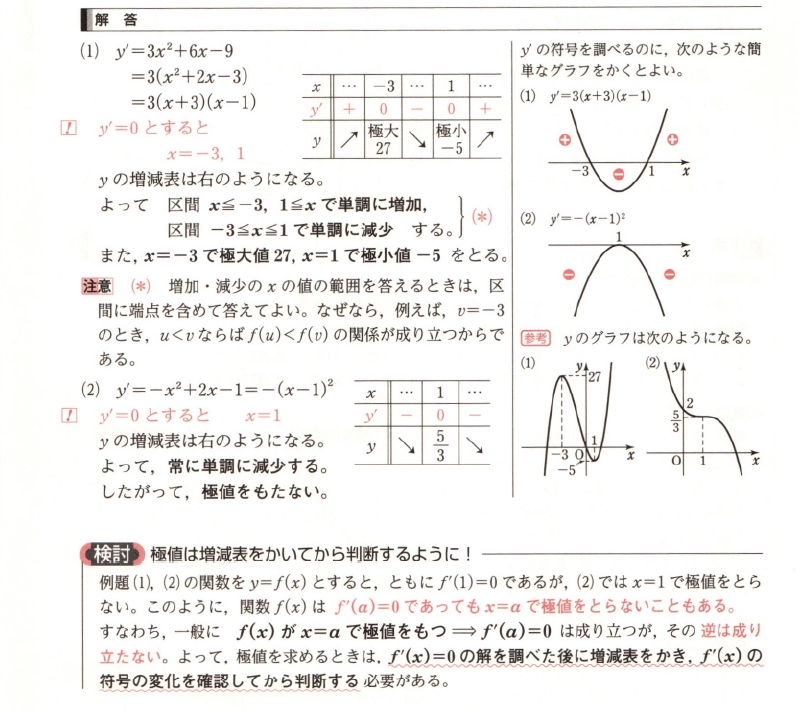
グラフにおいて「極値」と呼べるのは定義域の前後で微分係数が別符号でないといけないのね…。
例えば $ x = a $ のところでは微分係数が $ f'(a) = 0 $ であっても、その前後が ++ だと単調増加、-- だと単調減少と言う表現なんですね。
けっして「極値」とは言わないのですか…。
青チャート数学IIから参考になる 検討 を右に示しておきます。
高校時代にこのこと、習ったっけかなぁ…
まったく覚えていない。( ^^;
微分積分は楽しかったから、高校の授業中も集中して受けてたと思ったんですけどね…「極値」について正しく記憶してない自分にがっかりです。
ま、落ち込むほどのことじゃないけどね。
では今日も休日を始めています。休日の充実こそ、人生の充実です。
( ブログのコメント欄は 2022-04-16 に閉鎖いたしました )
今日は青チャート数学IIの微分法の中の "関数の増減と極大・極小" について学習をしていたのですが、その時にちょっとびっくりしました。

うーむ…そうなのか…。
グラフにおいて「極値」と呼べるのは定義域の前後で微分係数が別符号でないといけないのね…。
例えば $ x = a $ のところでは微分係数が $ f'(a) = 0 $ であっても、その前後が ++ だと単調増加、-- だと単調減少と言う表現なんですね。
けっして「極値」とは言わないのですか…。
青チャート数学IIから参考になる 検討 を右に示しておきます。
高校時代にこのこと、習ったっけかなぁ…
まったく覚えていない。( ^^;
微分積分は楽しかったから、高校の授業中も集中して受けてたと思ったんですけどね…「極値」について正しく記憶してない自分にがっかりです。
ま、落ち込むほどのことじゃないけどね。
では今日も休日を始めています。休日の充実こそ、人生の充実です。
( ブログのコメント欄は 2022-04-16 に閉鎖いたしました )
閲覧(6128)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



