時空 解 さんの日記
2024
8月
19
(月)
21:41
本文
皆さん こんにちは、時空 解です。
長いお盆休みの会社も、今日でほとんどが終わったのではないでしょうか。
私は先週の15日に "お盆休み的な日" を終え、16、17日とスポーツジムのプールに行って泳いできました。
でも毎週月曜日はスポーツジムのプールはお休み。私にとってもお休みの日と言う感じです。
でもね、やっぱり休むのはプールだけですね。
ブログの投稿は、やっぱり毎日やろうと思い立ちました。
と言うことで、今日はチャート式数学の学習で、見落としがちな "参考事項" に付いてブログに書いておきたいと思います。
--------------

皆さんは青チャート式数学に載っている "参考事項" にどう取り組んでいますか?
私は高校時代 (今までも) ただ目を通す…、いやいや。ただ眺めるだけで済ませていました。
これって、いわゆる "見流している" 状態ですよね。
パッと見て理解できる内容に付いては式変形の行間のようなところを頭の中で補って、内容を理解して行きますが…。
式変形が直ぐに分からないものとか、表記に馴染みのない物なんかは "見流して" いました。
でもね。
今回お目に掛かった "参考事項" は "見流して" しまうにはあまりにももったいない内容のものでした。
「部分分数分解をしてシグマ計算をすると、打ち消しあって、最初と最後だけが残る…」
これだけでも知的なおどろきがあったんですが。その続きもあるんですね。
関数式的 (?) なものにも、この発想を使った先人がいるんですね。(右画像)
今回の "参考事項" はそんな内容のものです。
この "参考事項" …。
なるほど下記の部分までで十分に知的欲求を満足させてくれます。

ですが続く【例】に出てくる式
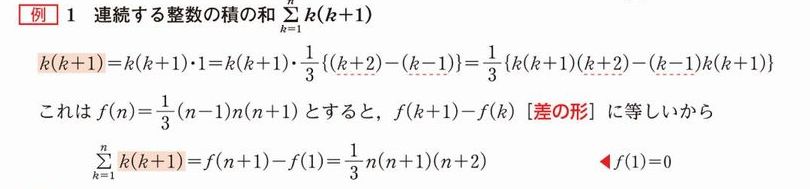
この羅列されて見難い (?) 式の "式変形の行間" を面倒臭がらずに埋めようとしたら…驚きました!
$ k(k+1) =k(k+1) \cdot 1 $
まずは、この式の最後の $ \cdot 1 $ って、どうしたら発想出来るんでしょうかね? ( ^^;
目標値としては
$ a_k = f{(k+1)} - f{(k)} $
があるのでしょうが…とても $ 1 $ を下記のように変形して登場させる発想は、私には絶対にありません。_| ̄|○
$ 1 = \displaystyle \frac{ 1 }{ 3 } \{ (k+2)-(k-1) \} $
この $ 1 $ を目的のものに変形する発想は "連続する整数が出てくればいい" 的なものだとは想像出来ますが…。
でも、$ k $、$ (k+1) $、$ (k+2) $ なんてものではなくて $ (k-1) $ なんてのが入っていますよね。
ここにたどり着くまでは、とても私的には考えられません。
こんなことを考えそうな先人って…いったい誰だ?
と思って、ちょっと調べて見たんですね。
"シグマ記号の歴史" なんて文字列で。
そしたらなんと!
…と言うよりかは、やっぱり! と言う感じかな…
シグマ記号を始めて使ったとされる歴史上の人物は
・オイラー
なんだそうです。(ニッセイ基礎研究所 より)
そう言われてみると、この式変形の発想…なんとなくオイラーっぽいですよね?!
この式変形がオイラーの物と決めつけてはいけませんが。
でも、式変形の行間を楽しむためについ筆記計算を始めてしまう…そんな精神状態になりたいものです。
でき今日はこんなところです。また明日
長いお盆休みの会社も、今日でほとんどが終わったのではないでしょうか。
私は先週の15日に "お盆休み的な日" を終え、16、17日とスポーツジムのプールに行って泳いできました。
でも毎週月曜日はスポーツジムのプールはお休み。私にとってもお休みの日と言う感じです。
でもね、やっぱり休むのはプールだけですね。
ブログの投稿は、やっぱり毎日やろうと思い立ちました。
と言うことで、今日はチャート式数学の学習で、見落としがちな "参考事項" に付いてブログに書いておきたいと思います。
--------------

皆さんは青チャート式数学に載っている "参考事項" にどう取り組んでいますか?
私は高校時代 (今までも) ただ目を通す…、いやいや。ただ眺めるだけで済ませていました。
これって、いわゆる "見流している" 状態ですよね。
パッと見て理解できる内容に付いては式変形の行間のようなところを頭の中で補って、内容を理解して行きますが…。
式変形が直ぐに分からないものとか、表記に馴染みのない物なんかは "見流して" いました。
でもね。
今回お目に掛かった "参考事項" は "見流して" しまうにはあまりにももったいない内容のものでした。
「部分分数分解をしてシグマ計算をすると、打ち消しあって、最初と最後だけが残る…」
これだけでも知的なおどろきがあったんですが。その続きもあるんですね。
関数式的 (?) なものにも、この発想を使った先人がいるんですね。(右画像)
今回の "参考事項" はそんな内容のものです。
この "参考事項" …。
なるほど下記の部分までで十分に知的欲求を満足させてくれます。

ですが続く【例】に出てくる式
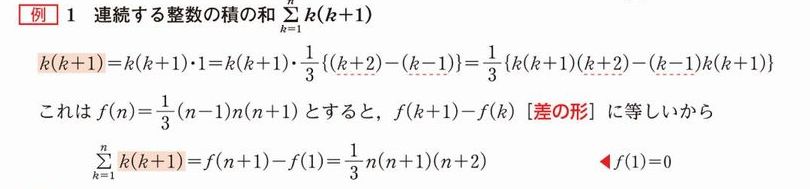
この羅列されて見難い (?) 式の "式変形の行間" を面倒臭がらずに埋めようとしたら…驚きました!
$ k(k+1) =k(k+1) \cdot 1 $
まずは、この式の最後の $ \cdot 1 $ って、どうしたら発想出来るんでしょうかね? ( ^^;
目標値としては
$ a_k = f{(k+1)} - f{(k)} $
があるのでしょうが…とても $ 1 $ を下記のように変形して登場させる発想は、私には絶対にありません。_| ̄|○
$ 1 = \displaystyle \frac{ 1 }{ 3 } \{ (k+2)-(k-1) \} $
この $ 1 $ を目的のものに変形する発想は "連続する整数が出てくればいい" 的なものだとは想像出来ますが…。
でも、$ k $、$ (k+1) $、$ (k+2) $ なんてものではなくて $ (k-1) $ なんてのが入っていますよね。
ここにたどり着くまでは、とても私的には考えられません。
こんなことを考えそうな先人って…いったい誰だ?
と思って、ちょっと調べて見たんですね。
"シグマ記号の歴史" なんて文字列で。
そしたらなんと!
…と言うよりかは、やっぱり! と言う感じかな…
シグマ記号を始めて使ったとされる歴史上の人物は
・オイラー
なんだそうです。(ニッセイ基礎研究所 より)
そう言われてみると、この式変形の発想…なんとなくオイラーっぽいですよね?!
この式変形がオイラーの物と決めつけてはいけませんが。
でも、式変形の行間を楽しむためについ筆記計算を始めてしまう…そんな精神状態になりたいものです。
でき今日はこんなところです。また明日
閲覧(6104)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



