時空 解 さんの日記
2021
2月
21
(日)
09:46
本文
皆さんこんにちは、時空 解です。
「実用数学技能検定要点整理2級」 の「7-2 ベクトルと図形」へと学習を進めています。
ここで気になる出題が一つ…
p149 に載っている「1次 重要」と示された下記の問題です。
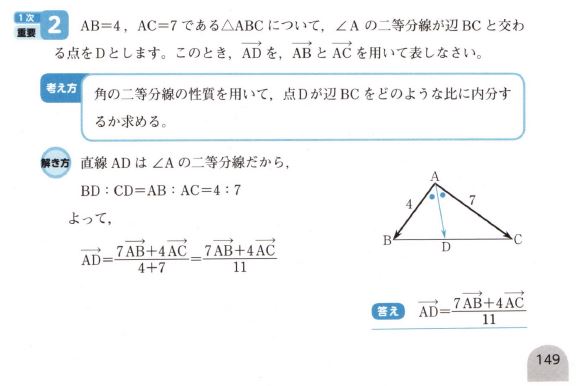
この問題の「考え方」のところに 角の二等分線の性質 を利用すると書かれていますが、"角の二等分線の性質" と言う文字列の掲載は、このテキスト内には、この問題と、後の練習問題にしか出てこないのです。
解説が無いんですよね。 (アクロバットファイル内上で文字列検索した結果です)
(アクロバットファイル内上で文字列検索した結果です)
内分点や外分点を求める公式の解説は check! としてまとめられていますけどね。
やはり図形となると、青チャート式数学Aに載っている定理1から定理18を一通り見ておいたほうが良さそうですかね?
(ちなみに、定理1が角の二等分線の性質です)
2級の過去問を調べてみないと何とも言えないことですけどね。
でも定理1~18と言うのは、私がちょうど学習していたところだったんです。対応する青チャート式数学Aの基本例題・重要例題は 基本例題64~90 になるでしょうかね…。
ここで定理1~18を書き並べられると良いのですが、今は時間がありませんので、また何かの機会に…。
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
「実用数学技能検定要点整理2級」 の「7-2 ベクトルと図形」へと学習を進めています。
ここで気になる出題が一つ…
p149 に載っている「1次 重要」と示された下記の問題です。

この問題の「考え方」のところに 角の二等分線の性質 を利用すると書かれていますが、"角の二等分線の性質" と言う文字列の掲載は、このテキスト内には、この問題と、後の練習問題にしか出てこないのです。
解説が無いんですよね。
内分点や外分点を求める公式の解説は check! としてまとめられていますけどね。
やはり図形となると、青チャート式数学Aに載っている定理1から定理18を一通り見ておいたほうが良さそうですかね?
(ちなみに、定理1が角の二等分線の性質です)
2級の過去問を調べてみないと何とも言えないことですけどね。
でも定理1~18と言うのは、私がちょうど学習していたところだったんです。対応する青チャート式数学Aの基本例題・重要例題は 基本例題64~90 になるでしょうかね…。
ここで定理1~18を書き並べられると良いのですが、今は時間がありませんので、また何かの機会に…。
では今日も1日の習慣を始めてます。小さな一歩・挑戦を試みています。
閲覧(8055)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



