50代から理数を学ぶ - 正弦定理・余弦定理と三角形の面積

トップ > ☆ 定理・公式 (見直しの習慣) > 正弦定理・余弦定理と三角形の面積 - ヘロンの公式、内接円 -

正弦定理・余弦定理と三角形の面積、ヘロンの公式

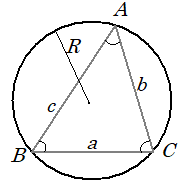
　　　正弦定理

$\triangle ABC$ において、

$BC = a,　CA = b,　AB = c$ 。

$\angle CAB = A,　\angle ABC =B,　\angle BCA = C$
外接円の半径を

$R$ とすると、

$2R$ =

$\displaystyle {\frac {a}{\sin A}} = \displaystyle {\frac {b}{\sin B}} = \displaystyle {\frac {c}{\sin C}}$ ○ 　　　 × Click! Anser

が成り立つ。

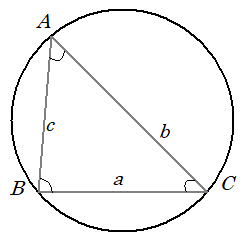
　　　余弦定理

$\triangle ABC$ において、

$BC = a,　CA = b,　AB = c$ 。

$\angle CAB = A,　\angle ABC =B,　\angle BCA = C$
とすると、

$a^2$ =

$b^2 + c^2 - 2bc \cdot \cos A$ ○ 　　　 × Click! Anser

$b^2$ =

$c^2 + a^2 - 2ca \cdot \cos B$ ○ 　　　 × Click! Anser

$c^2$ =

$a^2 + b^2 - 2ab \cdot \cos C$ ○ 　　　 × Click! Anser
が成り立つ。

また、下記のように変形した形も覚えておくとよい。

$\cos A$ =

$\displaystyle \frac{ b^2 + c^2 - a^2 }{ 2bc }$ ○ 　　　 × Click! Anser

$\cos B$ =

$\displaystyle \frac{ c^2 + a^2 - b^2 }{ 2ca }$ ○ 　　　 × Click! Anser

$\cos C$ =

$\displaystyle \frac{ a^2 + b^2 - c^2 }{ 2ab }$ ○ 　　　 × Click! Anser

　　　三角形の面積、ヘロンの公式

$\triangle ABC$ の面積を

$S$ 、

$BC = a,　CA = b,　AB = c$ 。

$\angle CAB = A,　\angle ABC =B,　\angle BCA = C$ とすると、

$S$ =

$\displaystyle { \frac{ 1 }{ 2 } bc \cdot \sin A = \frac{ 1 }{ 2 } ca \cdot \sin B = \frac{ 1 }{ 2 } ab \cdot \sin C }$ ○ 　　　 × Click! Anser

また、ヘロンの公式は

$S$ =

$\sqrt{ s(s - a)(s - b)(s - c) }$ ○ 　　　 × Click! Anser 　　　　　ただし

$s$ =

$\displaystyle \frac{ a + b + c }{ 2 }$ ○ 　　　 × Click! Anser

となる。

　　　三角形の内接円と面積

$\triangle ABC$ 、

$BC = a,　CA = b,　AB = c$ 。内接円の半径を

$r$ とすると

$S$ =

$\displaystyle \frac{ 1 }{ 2 } r (a+b+c)$ ○ 　　　 × Click! Anser

投票数:113 平均点:10.00

この記事の1行目に飛ぶ

三角関数の合成

☆ 定理・公式 (見直しの習慣)

ド・モルガンの法則、個数定理