出典、参考文献：数学I_数と式-08 を対象 (青チャート式数学公式集より)
 

$ acx^2 +(ad +bc)x +bd = (ax +b)(cx +d) $

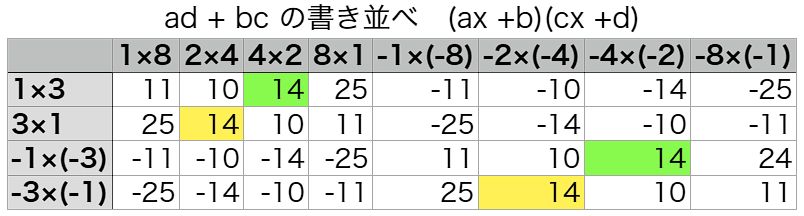
　例1：$ 3x^2 +14x +8 = (x +4)(3x +2) $

　例2：$ 84x^2 -19x -78 = (12x -13)(7x +6) $

　例3：$ 6x^2 +13xy +6y^2  = (3x +2y)(2x +3y) $


　例3：$ 6x^2 +13xy +6y^2  = (〇x +〇y)(〇x +〇y) $

　・$ 6 = 1 × 2 × 3 $、約数の数は $ 2^1 $、$ 3^1 $ より

　　　　　　　　　　　　$ (1+1)(1+1) = 4 $

　　　　　　　　　　　　約数は $ 1,~2,~3,~6 $




　　　$  \textcolor{gray}{ a　~~~b　　c　~~d　　ac　bd　　ad +bc} $

　例1：$ 3x^2 +14x +8 = (~1x +4)(3x +2)　　(〇x +〇)(〇x +〇) $

　・$ 3 = 1 × 3^{ \textcolor{blue}{1}} $、約数の数は $  \textcolor{blue}{1} +1 = 2 $　　約数は $ 1,~3 $

　　　　$ 1,~3 $ から $ \underline {3 = ac} $ となる $ a,~c $ の数を探る

　・$ 8 = 1 × 2^{ \textcolor{blue}{3}} $、約数の数は $ \textcolor{blue}{3} +1 = 4 $　　約数は $ 1,~2,~4, 8 $

　　　　$ 1,~2,~4,~8 $ から $ \underline {8 = bd} $ となる $ b,~d $ を探る


　・$ \underline {14 = ad +bc} $ となる $ a,~b,~c,~d $ の組み合わせを見つける
　　



　例2：$ 84x^2 -19x -78 = (12x -13)(7x +6) $

　・$ 84 = 1 ×2^{ \textcolor{blue}{2}} ×3^{ \textcolor{blue}{1}} × 7^{ \textcolor{blue}{1}} $、
　　　　　約数の数は $ (\textcolor{blue}{2} +1) \cdot (\textcolor{blue}{1} +1) \cdot (\textcolor{blue}{1} +1) = 12 $

　・$ 78 = 1 ×2^{ \textcolor{blue}{1}} × 3^{ \textcolor{blue}{1}} ×13^{ \textcolor{blue}{1}} $、
　　　　　約数の数は $ (\textcolor{blue}{1} +1) \cdot ( \textcolor{blue}{1} +1) \cdot (\textcolor{blue}{1} +1) = 8 $  
　
　



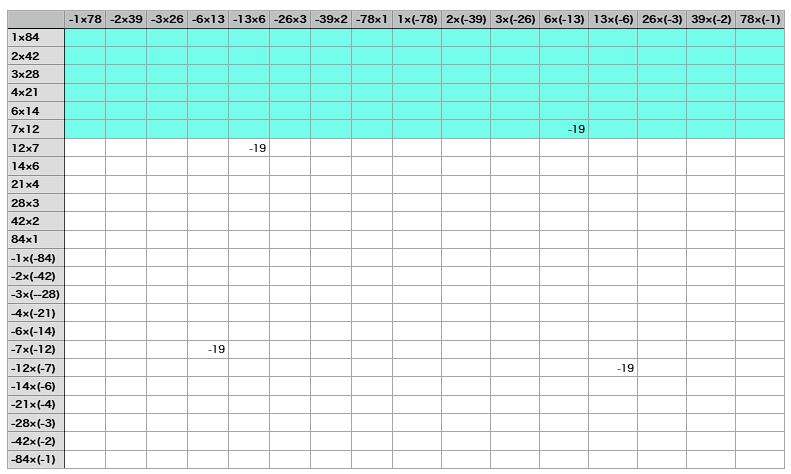
　例2：$ 84x^2 -19x -78 = (12x -13)(7x +6) $


２次方程式　$ ax^2 +bx +c = 0 $　の解の公式

$ x = \displaystyle \frac{ -b \pm \sqrt{ b^2 -4ac } }{ 2a } $　より

$ x = \displaystyle \frac{ -(-19) \pm \sqrt{ (-19)^2 -4 \cdot 84 \cdot (-78) } }{ 2 \cdot 84 } $

$ \therefore ~ x = \displaystyle \frac{ 13 }{ 12 },~- \frac{6}{7} $ なので

$ \left( x - \displaystyle \frac{ 13 }{ 12 } \right) \left( x  \displaystyle + \frac{ 6 }{ 7 } \right) = 0 $　両辺に $ 12 \cdot 7 $ を掛けると

　$ (12x -13)( 7x +6) = 0 $