集合の要素の個数
ここには確率を求める時に利用する、集合論の内容をまとめてある。
集合とその表し方
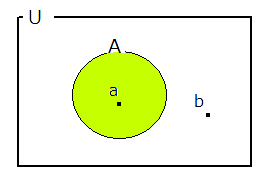 集合とは、はっきりと区別できる「もの」の集まりである。集合を構成する「もの」を要素または元という。
集合とは、はっきりと区別できる「もの」の集まりである。集合を構成する「もの」を要素または元という。
集合を $ A $ 、集合を構成する「もの」を $ a $ 、構成しない「もの」を $ b $ とすると
・$ a \in A $ … $ a $ は集合 $ A $ の要素である。
$ a $ は集合 $ A $ に属する。
・$ b \notin A $ … $ b $ は集合 $ A $ の要素ではない。
$ b $ は集合 $ A $ に属さない。
集合を表すのに、2種類の記述法がある。
・要素を並べて表す方法 … $ \{1,~3,~5 \} $
$ \{x^2,~3xy+1,~y \} $ など
・集合の要素になる条件を書く方法 … $ \{n \mid n $ は $ 5 $ 以下の自然数 $ \} $
$ \{x^2+1 \mid x $ は $ 1 \lt x \lt 3 $ なる実数 $ \} $ など
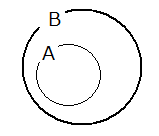
部分集合
集合 $ A $ が集合 $ B $ に含まれる時、または集合 $ B $ が集合 $ A $ を含むとき
・$ A \subset B $ …集合 $ A $ は集合 $ B $ の部分集合である。
「$ x \in A $ ならば $ x \in B $ 」が成り立つ。
$ A $ と $ B $ のそれぞれの要素が等しいとき
・$ A = B $ …集合 $ A $ と集合 $ B $ の要素は完全に一致する。
「$ A \subset B $ かつ $ B \subset A $ 」が成り立つ。
集合が「もの」を1つも含まないとき
・空集合 $ \varnothing $
- 注意 -
・集合 $ A $ は集合 $ A $ 自身の部分集合でもある。すなわち $ A \subset A $
・空集合 $ \varnothing $ はすべての集合の部分集合とも考えられる。
共通部分、和集合
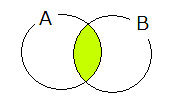
・$ A \cap B $
上記はすなわち $ A \cap B = \{x \mid x \in A $ かつ $ x \in B \} $ である。
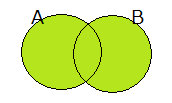
・$ A \cup B $
上記はすなわち $ A \cup B = \{x \mid x \in A $ または $ x \in B \} $ である。
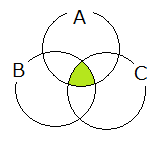
・$ A \cap B \cap C $
上記はすなわち $ A \cap B \cap C = \{x \mid x \in A $ かつ $ x \in B $ かつ $ x \in C \} $ である。
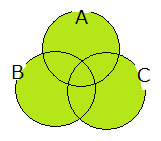
・$ A \cup B \cup C $
上記はすなわち $ A \cup B \cup C = \{x \mid x \in A $ または $ x \in B $ または $ x \in C \} $ である。
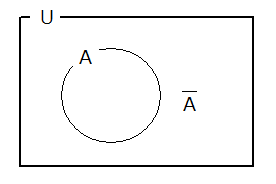
補集合
全体の集合 $ U $ の要素で、$ A $ に属さない要素全体の集合を補集合と言う。この集合を下記の記号で表す。
・$ \bar{ A } $
$ A \cap \bar{ A } = \varnothing $
$ A \cup \bar{ A } = U $
$ \overline{ \overline{ A } } = A $
|
実数、絶対値、平方根 |
☆ 定義 (Anser 形式) |





