時空 解 さんの日記
2019
9月
14
(土)
09:12
本文
皆さん、おはようございます。時空 解です。
新しい腰掛と新しいモニターと、それと模様替え途中の部屋もずいぶんと整ってきました。朝もそれなりに6時台に起きれるようになってきました。これから数学の学習に集中できそうです。
さて、さっそく昨日は数検2級の学習を始めたのですが…三角比のところで早くも壁にぶつかりました。
みなさんは下記の問題、直ぐにわかりますか?
みなさんは下記の問題、直ぐにわかりますか?
次の計算をしなさい
$ \sin 110^\circ + \cos 160^\circ $
$ \sin 110^\circ + \cos 160^\circ $
この問題は、私の作ったコンテンツ「三角比の基本定理」が分っている方ならわかる問題です。コンテンツを作った私本人も直ぐに分からなくてはいけないのです。
でも、なかなかわかりませんでした。
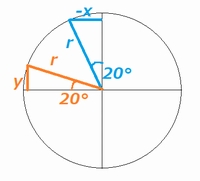
単位円に書いてみれば、パッと見、直ぐにブラスとマイナスの関係になっていると分かります。ですから打ち消し合って0(ゼロ) になる事は見て取れますよね。
でも、この手の問題が数検の2次の問題として出題された場合、その計算過程も記述しなくてはなりません。
でも、なかなかわかりませんでした。

単位円に書いてみれば、パッと見、直ぐにブラスとマイナスの関係になっていると分かります。ですから打ち消し合って0(ゼロ) になる事は見て取れますよね。
でも、この手の問題が数検の2次の問題として出題された場合、その計算過程も記述しなくてはなりません。
単位円の図を描いて
「$ \sin 110^\circ $ はオレンジ色の $ \displaystyle \frac{ y }{ r } $、$ \cos 160^\circ $ はブルーの $ \displaystyle - \frac{ x }{ r } $ 。ここで $ x $ と $ y $ は同じ長さなので、0」
なーんて解答を書いても点数はもらえないでしょう。
「$ \sin 110^\circ $ はオレンジ色の $ \displaystyle \frac{ y }{ r } $、$ \cos 160^\circ $ はブルーの $ \displaystyle - \frac{ x }{ r } $ 。ここで $ x $ と $ y $ は同じ長さなので、0」
なーんて解答を書いても点数はもらえないでしょう。
やっぱりここは三角比の基本定理を持ち出して、$ \sin 110^\circ $ と $\cos 160^\circ $ を変形するしかありません。
やろうとしたら…
難しい!
やろうとしたら…
難しい!
昨日は、この変形を記述するのに四苦八苦しました。「三角比の基本定理」をどう利用すればいいのか、その選択に迷います。
90° を引くのか足すのか、180° を引くのか足すのか。
それに $ \sin 110^\circ $ と $\cos 160^\circ $ をサインに統一するのかコサインか? それにも迷います。
結局
$ \sin 110^\circ = \sin {(180^\circ - 70^\circ)} = \sin 70^\circ = \sin {(90^\circ - 20^\circ)} = \cos 20^\circ $
$ \cos 160^\circ = \cos {(180^\circ - 20^\circ)} = - \cos 20^\circ $
となりますが…。
90° を引くのか足すのか、180° を引くのか足すのか。
それに $ \sin 110^\circ $ と $\cos 160^\circ $ をサインに統一するのかコサインか? それにも迷います。
結局
$ \sin 110^\circ = \sin {(180^\circ - 70^\circ)} = \sin 70^\circ = \sin {(90^\circ - 20^\circ)} = \cos 20^\circ $
$ \cos 160^\circ = \cos {(180^\circ - 20^\circ)} = - \cos 20^\circ $
となりますが…。
学生の頃なら直ぐに出来た気がするんです。「自分は歳を取ったかな?」なんて言葉が頭をよぎります…。
でも、本当は歳のせいではないんでしょうけどね。
きっと性格のせいです。思い出してみると、学生の頃は図的に分かればそれで良しとしてようなきがします。
きっと性格のせいです。思い出してみると、学生の頃は図的に分かればそれで良しとしてようなきがします。
先に示した図を描いて
「よし、これで自分は解っている。俺は点取り虫ではないからテストで点数取れなくても良し!」
なーんて考えるタチでした。
「よし、これで自分は解っている。俺は点取り虫ではないからテストで点数取れなくても良し!」
なーんて考えるタチでした。
ふざけていたなぁ…自分。これも因数分解と同じで、簡単な問題をたくさん解いて行かないと、頭の中にイメージが造られないのでしょうね。
数学は人と知的な事柄を伝え合うための道具です。人と一緒の表現方法を身に付けなくてはね、自己満足に陥ります。
では今日も1日の習慣を始めます。小さな一歩・挑戦を試みます。
応援してね。
千里の道も一歩から。そしてその道は登り坂です。ローマは1日にして成らず、です。
(ポチッとブログ村のバナーをクリックしてね) ![]()
![]()
| ★ 平日を充実させるために… | ☆ 実施状況 |
|---|---|
| 数学の問題 1問 (物理学の数式の理解力の獲得) ランチ前 |
チャート式 数学 白II+B:せず チャート式 数学 青I+A:p422, p423 実用数学技能検定 要点整理2級:p62~p65 スタディサプリ:せず 数学の答え合わせは後でまとめてやる:〇 数学の学習に取り組んだ時間:1時間15分 |
| 2階に上り降り時、懸垂1回 (ボルダリングの体力獲得) ランチ & 買い物前 |
できず |
| コンテンツ1つ、小説1節 ランチ & 買い物後 |
コンテンツ できず 小説1節 できず |
| そろばんの練習5問 (暗算の獲得) 夜、寝る前 |
加減算 できず 掛け算 せず |
| 規則正しい休日の生活 基本習慣 |
昨日・寝床に入った時間:22時40分 今朝・7時に布団から出る:06時35分 朝 --- ブログの投稿 --- |
閲覧(8631)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



