時空 解 さんの日記
2023
3月
23
(木)
09:20
本文
皆さんこんにちは、時空 解です。
昨日、我が家の郵便受けに 第404回 数学検定 の結果が届いていました。
さっそく中身を確認してみると…1次も2次も全体の平均点よりも下。
ガックリです。_| ̄|○
まぁでも
「こんな回もあるさ」
と言うことで、出来なかった問題の見直しをしているところです。(前を向いて行かないとね)
まずは1次のこの因数分解。
答え:$ (x - 2y)(x + 2y + 5) $ ○ × Click! Anser
これって、どんなアプローチの仕方で解くんですかね? ( ^^;
一般的には次数の小さい変数に着目して整理するやり方でしょうけど。(全体の正答率は 67.0 % です)
まぁこの問題2は出来なくても仕方ないとして、次の問題3を間違えてしまった私です。
答え: $ \sqrt{3} $ ○ × Click! Anser
この問題は受験当日、パッと見て
「あ、時間が掛かりそうだ」
と思い込んでしまった問題でした。
でも今日 冷静に式変形をしてみたら案外簡単でした。うーむ…私はやっぱり計算能力が低いと言うことかな…計算能力を磨かないとね。
それから問題5と6も出来なかったのですが…お恥ずかしい限りです。これは基本事項をちゃんと復習してないからですね。
答え: $ 14 $ ○ × Click! Anser
こんなの三角比の性質が分かっていれば、公式 $ \displaystyle \frac{ 1 }{ 2 } \cdot BC \cdot AB \cdot \sin B $ を知らなくても解ける問題です。
どうして解けなかったのだろう。( ^^;
答え:$ 85^\circ $ ○ × Click! Anser
これも円に内接する四角形の性質 (対角の和は $ 180^\circ $ ) そのものです。
図形の性質の公式として分かっていないとね…
「対角の合計は $ 180^\circ $ になるんだっけかなぁ…」
と思ったんで、書けば良かったですね。ハッキリしないと書かない自分もダメですね、なんだか卑怯なきがしてね。
この "円に内接する四角形の性質" は数研出版(株)さんのデジタル副教材
「青チャート数学I+A」
の公式集にもちゃんと出てきます。( ^^;
さて、今日のところはこの辺にしておきましょう。
☆ アンサーボタンについては こちら を参照してください
では今日も休日を始めています。休日の充実こそ、人生の充実です。
( ブログのコメント欄は 2022-04-16 に閉鎖いたしました )
昨日、我が家の郵便受けに 第404回 数学検定 の結果が届いていました。
さっそく中身を確認してみると…1次も2次も全体の平均点よりも下。
ガックリです。_| ̄|○
まぁでも
「こんな回もあるさ」
と言うことで、出来なかった問題の見直しをしているところです。(前を向いて行かないとね)
まずは1次のこの因数分解。
第404回 数学検定 2級1次、問題2
次の式を因数分解しなさい。
$ x^2 - 4y^2 + 5x - 10y $
次の式を因数分解しなさい。
$ x^2 - 4y^2 + 5x - 10y $
答え:$ (x - 2y)(x + 2y + 5) $ ○ × Click! Anser
これって、どんなアプローチの仕方で解くんですかね? ( ^^;
一般的には次数の小さい変数に着目して整理するやり方でしょうけど。(全体の正答率は 67.0 % です)
まぁこの問題2は出来なくても仕方ないとして、次の問題3を間違えてしまった私です。
第404回 数学検定 2級1次、問題3
次の計算をしなさい。答えが分数になるときは、分母を有理化して答えなさい。
$ \displaystyle \frac{ 2 }{ 1+ \sqrt{3} } + \frac{ 3 }{ 2 + \sqrt{2} } + \frac{ 1 }{ 4 + 3 \sqrt{2} } $
次の計算をしなさい。答えが分数になるときは、分母を有理化して答えなさい。
$ \displaystyle \frac{ 2 }{ 1+ \sqrt{3} } + \frac{ 3 }{ 2 + \sqrt{2} } + \frac{ 1 }{ 4 + 3 \sqrt{2} } $
答え: $ \sqrt{3} $ ○ × Click! Anser
この問題は受験当日、パッと見て
「あ、時間が掛かりそうだ」
と思い込んでしまった問題でした。
でも今日 冷静に式変形をしてみたら案外簡単でした。うーむ…私はやっぱり計算能力が低いと言うことかな…計算能力を磨かないとね。
それから問題5と6も出来なかったのですが…お恥ずかしい限りです。これは基本事項をちゃんと復習してないからですね。
第404回 数学検定 2級1次、問題5
$ AB = 5 $、$ BC = 8 $、$ \sin B = \displaystyle \frac{ 7 }{ 10 } $ である $ \triangle ABC $ の面積を求めなさい。
$ AB = 5 $、$ BC = 8 $、$ \sin B = \displaystyle \frac{ 7 }{ 10 } $ である $ \triangle ABC $ の面積を求めなさい。
答え: $ 14 $ ○ × Click! Anser
こんなの三角比の性質が分かっていれば、公式 $ \displaystyle \frac{ 1 }{ 2 } \cdot BC \cdot AB \cdot \sin B $ を知らなくても解ける問題です。
どうして解けなかったのだろう。( ^^;

第404回 数学検定 2級1次、問題6
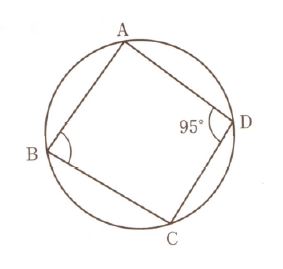
右の図のように、四角形 $ ABCD $ が円に内接しています。
$ \angle CDA = 95^\circ $ のとき、$ \angle ABC $ の大きさを求めなさい。
右の図のように、四角形 $ ABCD $ が円に内接しています。
$ \angle CDA = 95^\circ $ のとき、$ \angle ABC $ の大きさを求めなさい。
答え:$ 85^\circ $ ○ × Click! Anser
これも円に内接する四角形の性質 (対角の和は $ 180^\circ $ ) そのものです。
図形の性質の公式として分かっていないとね…
「対角の合計は $ 180^\circ $ になるんだっけかなぁ…」
と思ったんで、書けば良かったですね。ハッキリしないと書かない自分もダメですね、なんだか卑怯なきがしてね。
この "円に内接する四角形の性質" は数研出版(株)さんのデジタル副教材
「青チャート数学I+A」
の公式集にもちゃんと出てきます。( ^^;
さて、今日のところはこの辺にしておきましょう。
☆ アンサーボタンについては こちら を参照してください
では今日も休日を始めています。休日の充実こそ、人生の充実です。
( ブログのコメント欄は 2022-04-16 に閉鎖いたしました )
閲覧(6414)
| コメントを書く |
|---|
|
コメントを書くにはログインが必要です。 |





 前の日記
前の日記



